Feasibility relationships as Bool-profunctors

Feasilibiliy relation(1)

A feasibility relation for preorder \(X\) given preorder \(Y\)

Linked by

Exercise 4-4(2)

Suppose we have the preorders \(X:=\boxed{monoid\rightarrow category \leftarrow preorder}, Y:=\boxed{nothing \rightarrow thisBook}\)

  1. Draw the Hasse diagram for the preorder \(X^{op} \times Y\)

  2. Write a profunctor \(X \overset{\phi}\nrightarrow Y\)

    • True means “my aunt can explain an x given y"

    • Interpret the fact that the preimage of true is an upper set in \(X^{op}\times Y\)

Solution(1)

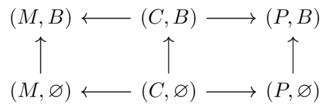
  2. Let \(\phi((M,B))=\phi((P,B))=True\) else \(False\)

    • The preimage of true being an upper set is a consequence of monotone maps to Bool. The domain orders combinations by feasibility (\(x\leq y\) means x is easier than y), and the preimage being an upper set says that if my aunt can explain \(x\) given \(y\), then she can do something easier than \(x\) given \(y\) and can explain \(x\) with something with more explanatory power than \(y\).

Exercise 4-7(2)

Show that the Boolean \(\Rightarrow\) satsifies the requirements of a closure operator.

Solution(1)

This boils down to the tautology that \((a \land v) \implies w\) iff \(a \implies (v \implies w)\), where the last \(\implies\) comes from \(\multimap\) and the others come from \(\leq\).